Vector Coordinates Plane Drawing Tool

In the introduction to vectors, we discussed vectors without reference to whatever coordinate system. Past working with just the geometric definition of the magnitude and direction of vectors, we were able to define operations such as improver, subtraction, and multiplication by scalars. We as well discussed the properties of these operation.

Oftentimes a coordinate system is helpful considering it can be easier to dispense the coordinates of a vector rather than manipulating its magnitude and direction directly. When we limited a vector in a coordinate system, we identify a vector with a listing of numbers, called coordinates or components, that specify the geometry of the vector in terms of the coordinate organisation. Hither nosotros will discuss the standard Cartesian coordinate systems in the plane and in 3-dimensional space.

Vectors in the airplane

Nosotros assume that you are familiar with the standard $(x,y)$ Cartesian coordinate arrangement in the plane. Each indicate $\vc{p}$ in the plane is identified with its $x$ and $y$ components: $\vc{p} = (p_1,p_2)$.

To determine the coordinates of a vector $\vc{a}$ in the plane, the offset step is to translate the vector and so that its tail is at the origin of the coordinate system. Then, the head of the vector volition be at some point $(a_1,a_2)$ in the airplane. Nosotros call $(a_1,a_2)$ the coordinates or the components of the vector $\vc{a}$. We often write $\vc{a} \in \R^2$ to announce that it tin be described by two real coordinates.

Using the Pythagorean Theorem, we tin can obtain an expression for the magnitude of a vector in terms of its components. Given a vector $\vc{a}=(a_1,a_2)$, the vector is the hypotenuse of a right triangle whose legs are length $a_1$ and $a_2$. Hence, the length of the vector $\vc{a}$ is $$\|\vc{a}\| = \sqrt{a_1^2+a_2^2}.$$

As an instance, consider the vector $\vc{a}$ represented by the line segment which goes from the point $(ane,ii)$ to the bespeak $(4,6)$. Can you calculate the coordinates and the length of this vector?

To find the coordinates, interpret the line segment i unit left and two units downwardly. The line segment begins at the origin and ends at $(4-ane,half-dozen-2) = (3,iv)$. Therefore, $\vc{a} = (3,iv)$. The length of $\vc{a}$ is $\|\vc{a}\| = \sqrt{3^2+4^ii} = v$.

The beneath applet, repeated from the vector introduction, allows you to explore the relationship between a vector's components and its magnitude.

The magnitude and management of a vector. The blue arrow represents a vector $\vc{a}$. The 2 defining backdrop of a vector, magnitude and direction, are illustrated past a ruby-red bar and a green arrow, respectively. The length of the red bar is the magnitude $\|\vc{a}\|$ of the vector $\vc{a}$. The light-green arrow always has length i, but its direction is the direction of the vector $\vc{a}$. The i exception is when $\vc{a}$ is the nothing vector (the just vector with zero magnitude), for which the management is non defined. Yous tin change either end of $\vc{a}$ past dragging it with your mouse. Yous tin can besides motility $\vc{a}$ by dragging the middle of the vector; yet, changing the position of the $\vc{a}$ in this style does not alter the vector, as its magnitude and direction remain unchanged.

More information nigh applet.

The vector operations we defined in the vector introduction are easy to express in terms of these coordinates. If $\vc{a}=(a_1,a_2)$ and $\vc{b}=(b_1,b_2)$, their sum is merely $\vc{a}+\vc{b}=(a_1+b_1,a_2+b_2)$, as illustrated in the beneath effigy. It is as well easy to encounter that $\vc{b}-\vc{a} = (b_1-a_1,b_2-a_2)$ and $\lambda \vc{a} = (\lambda a_1, \lambda a_2)$ for any scalar $\lambda$.

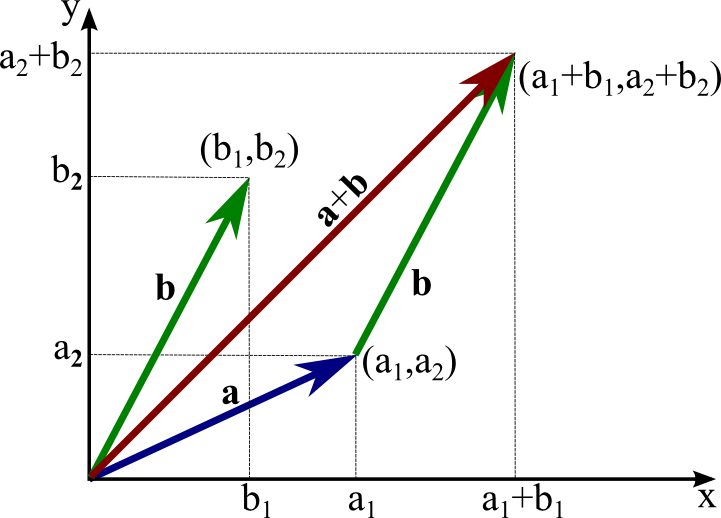
The beneath applet, also repeated from the vector introduction, allows you to explore the human relationship betwixt the geometric definition of vector add-on and the summation of vector components.

The sum of two vectors. The sum $\vc{a}+\vc{b}$ of the vector $\vc{a}$ (bluish arrow) and the vector $\vc{b}$ (scarlet arrow) is shown past the light-green arrow. Equally vectors are independent of their starting position, both blue arrows represent the same vector $\vc{a}$ and both cherry-red arrows represent the aforementioned vector $\vc{b}$. The sum $\vc{a}+\vc{b}$ can be formed past placing the tail of the vector $\vc{b}$ at the head of the vector $\vc{a}$. Equivalently, it tin can be formed by placing the tail of the vector $\vc{a}$ at the head of the vector $\vc{b}$. Both constructions together form a parallelogram, with the sum $\vc{a}+\vc{b}$ existence a diagonal. (For this reason, the commutative police force $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ is sometimes called the parallelogram law.) You can alter $\vc{a}$ and $\vc{b}$ by dragging the yellowish points.

More than information most applet.

Yous may accept noticed that nosotros utilise the aforementioned notation to denote a point and to denote a vector. We don't tend to emphasize any stardom between a indicate and a vector. Yous can think of a betoken as being represented past a vector whose tail is fixed at the origin. You'll have to figure out by context whether or not we are thinking of a vector equally having its tail fixed at the origin.

Another way to denote vectors is in terms of the standard unit of measurement vectors denoted $\vc{i}$ and $\vc{j}$. A unit vector is a vector whose length is one. The vector $\vc{i}$ is the unit vector in the direction of the positive $x$-axis. In coordinates, we can write $\vc{i}=(1,0)$. Similarly, the vector $\vc{j}$ is the unit of measurement vector in the direction of the positive $y$-axis: $\vc{j}=(0,1)$. Nosotros tin write any two-dimensional vector in terms of these unit vectors equally $\vc{a}=(a_1,a_2) = a_1\vc{i}+a_2\vc{j}$.

Vectors in three-dimensional infinite

In three-dimensional infinite, there is a standard Cartesian coordinate system $(x,y,z)$. Starting with a bespeak which we call the origin, construct 3 mutually perpendicular axes, which nosotros call the $10$-axis, the $y$-axis, and the $z$-axis. Hither is ane way to picture these axes. Stand near the corner of a room and look down at the point where the walls meet the flooring. So, the flooring and the wall to your left intersect in a line which is the positive $x$-axis. The floor and the wall to your right intersect in a line which is the positive $y$-centrality. The walls intersect in a vertical line which is the positive $z$-centrality. These positive axes are depicted in the beneath applet labeled past $x$, $y$, and $z$. The negative part of each axis is on the opposite side of the origin, where the axes intersect.

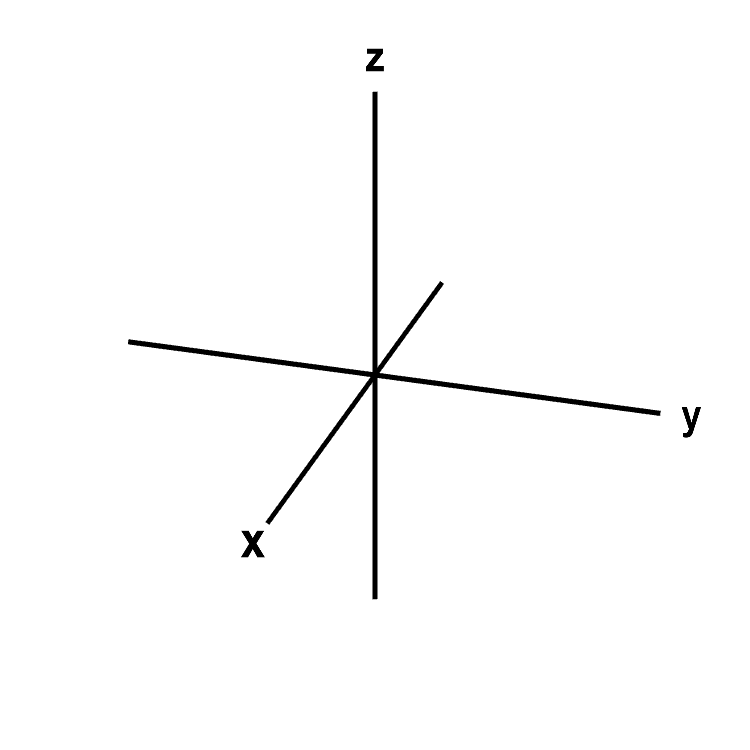
Applet loading

Three-dimensional Cartesian coordinate axes. A representation of the three axes of the iii-dimensional Cartesian coordinate organization. The positive $x$-axis, positive $y$-axis, and positive $z$-axis are the sides labeled by $ten$, $y$ and $z$. The origin is the intersection of all the axes. The co-operative of each centrality on the opposite side of the origin (the unlabeled side) is the negative part. Yous tin drag the figure with the mouse to rotate it.

More information about applet.

We have fix the relative locations of the positive $x$, $y$, and $z$-axis to make the coordinate system a right-handed coordinate system. Note that if you ringlet the fingers of your right manus from the positive $x$-axis to the positive $y$-axis, the thumb of your right mitt points in the direction of the positive $z$-axis.

If you lot switched the locations of the positive $x$-axis and positive $y$-axis, then you would stop up having a left-handed coordinate arrangement. If you do that, you lot volition be living in a mathematical universe in which some formulas will differ by a minus sign from the formula in the universe nosotros are using here. Your universe will exist merely as valid as ours, simply in that location will be lots of confusion. We propose you live in our universe while studying from these pages.

With these axes any betoken $\vc{p}$ in space can be assigned three coordinates $\vc{p}=(p_1,p_2,p_3)$. For case, given the above corner-of-room illustration, suppose you lot commencement at the corner of the room and motility four meters along the $ten$-axis, and then plough left and walk iii meters into the room. If y'all are ii meters tall, then the top of your caput is at the point $(4,3,2)$.

Simply every bit in two-dimensions, we assign coordinates of a vector $\vc{a}$ by translating its tail to the origin and finding the coordinates of the indicate at its head. In this way, we tin can write the vector as $\vc{a}=(a_1,a_2,a_3)$. We oft write $\vc{a} \in \R^3$ to announce that it tin exist described by three existent coordinates. Sums, differences, and scalar multiples of three-dimensional vectors are all performed on each component. If $\vc{a}=(a_1,a_2,a_3)$ and $\vc{b}=(b_1,b_2,b_3)$, then $\vc{a}+\vc{b}=(a_1+b_1,a_2+b_2,a_3+b_3)$, $\vc{b}-\vc{a}=(b_1-a_1,b_2-a_2,b_3-a_3)$, and $\lambda\vc{a}=(\lambda a_1, \lambda a_2, \lambda a_3)$.

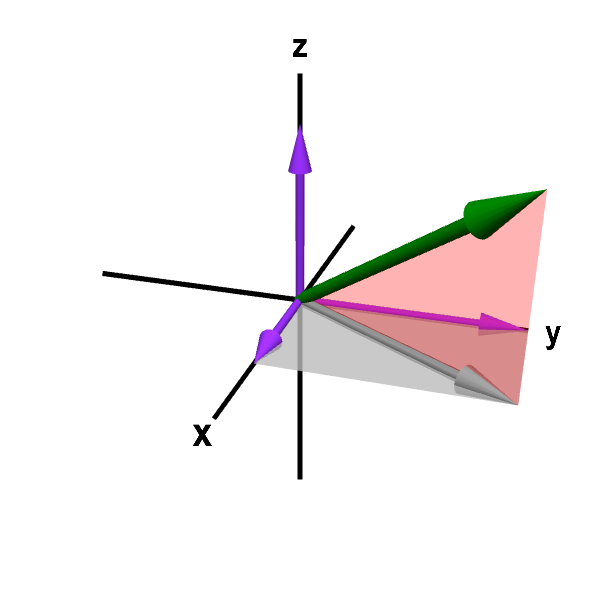
Applet loading

A vector in iii-dimensional space. A representation of a vector $\vc{a}=(a_1,a_2,a_3)$ in the three-dimensional Cartesian coordinate system. The vector $\vc{a}$ is drawn as a light-green arrow with tail fixed at the origin. You can drag the head of the dark-green arrow with your mouse to alter the vector. To help bear witness the 3 dimensional perspective, a pink triangle connects the vector to its projection $(a_1,a_2,0)$ in the $xy$-aeroplane (gray arrow). Purple vectors show the projections of $\vc{a}$ on each axis and represent the coordinates $a_1$, $a_2$, and $a_3$. Yous can also elevate the heads of the majestic vectors to alter but one of the coordinates of the vector. Or elevate the head of the gray vector in the $xy$-aeroplane to change just the $ten$ and $y$ coordinates.

More information about applet.

Merely as in two dimensions, we can as well denote iii-dimensional vectors is in terms of the standard unit vectors, $\vc{i}$, $\vc{j}$, and $\vc{grand}$. These vectors are the unit of measurement vectors in the positive $10$, $y$, and $z$ management, respectively. In terms of coordinates, nosotros can write them equally $\vc{i}=(1,0,0)$, $\vc{j}=(0,1,0)$, and $\vc{k}=(0,0,1)$. We can express any three-dimensional vector every bit a sum of scalar multiples of these unit vectors in the form $\vc{a}=(a_1,a_2,a_3) = a_1\vc{i}+a_2\vc{j}+a_3\vc{k}$.

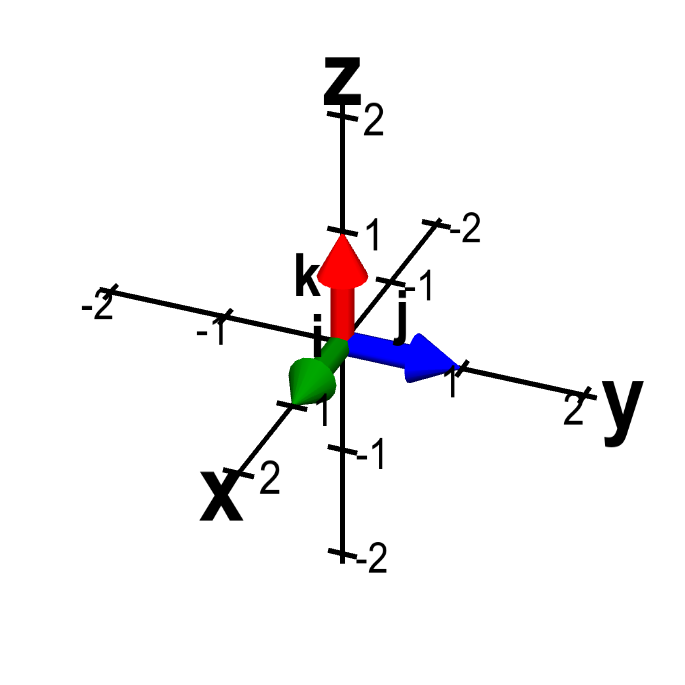
Applet loading

The standard unit vectors in iii dimensions. The standard unit vectors in three dimensions, $\vc{i}$ (green), $\vc{j}$ (blue), and $\vc{chiliad}$ (reddish) are length i vectors that betoken parallel to the $x$-axis, $y$-axis, and $z$-centrality respectively. Moving them with the mouse doesn't change the vectors, as they ever point toward the positive direction of their corresponding axis.

More information about applet.

What is the length of the vector $\vc{a}=(a_1,a_2,a_3)$? We can decompose the vector into $(a_1,a_2,a_3) = (a_1,a_2,0)+(0,0,a_3)$, where the two vectors on the right hand side correspond to the two light-green line segments in the in a higher place applet. These ii line segments form a correct triangle whose hypotenuse is the vector $\vc{a}$ (the blueish line segment). The first vector can be thought of every bit a two dimensional vector, so its length is $\|(a_1,a_2,0)\| = \|(a_1,a_2)\| = \sqrt{a_1^2+a_2^ii}$. The 2d vector's length is $\|(0,0,a_3)\| = |a_3|$. Therefore, by the Pythagorean Theorem, the length of $\vc{a}$ is $$\|\vc{a}\| = \sqrt{\|(a_1,a_2,0)\|^two + \|(0,0,a_3)\|^2} = \sqrt{a_1^2+a_2^2+a_3^two}.$$

Going across iii dimensions?

Nosotros can easily visualize 2 or three dimensions past drawing pictures of a aeroplane or of space. If we represent a vector by a list of numbers such as $(a_1,a_2) \in \R^2$ and $(a_1,a_2,a_3) \in \R^3$, we can easily go beyond 3 dimensions into four dimensions $(a_1,a_2,a_3,a_4) \in \R^4$ or even to arbitrary dimension such as $northward$-dimensions $(a_1,a_2, \ldots, a_n) \in \R^n$, where $northward$ is some positive integer.

Going to college dimension is easy with lists of numbers, though of course high-dimensional vectors are not easy (not possible?) to visualize. You tin can read more than nearly high-dimensional vectors or check out examples of $northward$-dimensional vectors that illustrate how going to dimensions higher than three can be useful in many situations.

`

crothersnuied1997.blogspot.com

Source: https://mathinsight.org/vectors_cartesian_coordinates_2d_3d

Share this post